Computes eigenvalues and eigenvectors of a real (non-complex) matrix. More...

#include <Bpp/Numeric/Matrix/EigenValue.h>

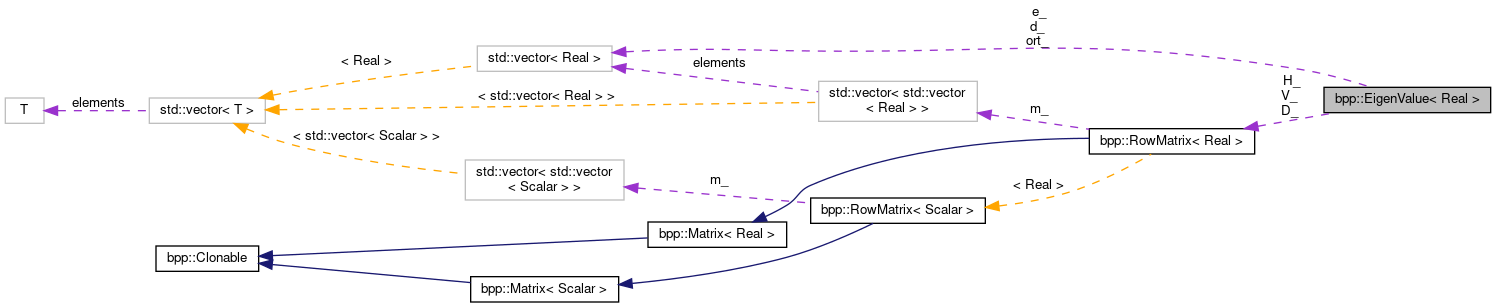
Collaboration diagram for bpp::EigenValue< Real >:

Public Member Functions
bool	isSymmetric () const

	EigenValue (const Matrix< Real > &A)
	Check for symmetry, then construct the eigenvalue decomposition. More...

const RowMatrix< Real > &	getV () const
	Return the eigenvector matrix. More...

const std::vector< Real > &	getRealEigenValues () const
	Return the real parts of the eigenvalues. More...

const std::vector< Real > &	getImagEigenValues () const
	Return the imaginary parts of the eigenvalues in parameter e. More...

const RowMatrix< Real > &	getD () const
	Computes the block diagonal eigenvalue matrix. More...

Private Member Functions
void	tred2 ()
	Symmetric Householder reduction to tridiagonal form. More...

void	tql2 ()
	Symmetric tridiagonal QL algorithm. More...

void	orthes ()
	Nonsymmetric reduction to Hessenberg form. More...

void	cdiv (Real xr, Real xi, Real yr, Real yi)

void	hqr2 ()

Private Attributes
size_t	n_
	Row and column dimension (square matrix). More...

bool	issymmetric_
	Tell if the matrix is symmetric. More...

RowMatrix< Real >	V_
	Array for internal storage of eigenvectors. More...

RowMatrix< Real >	H_
	Matrix for internal storage of nonsymmetric Hessenberg form. More...

RowMatrix< Real >	D_
	Matrix for internal storage of eigen values in a matrix form. More...

std::vector< Real >	ort_
	Working storage for nonsymmetric algorithm. More...

Real	cdivr

Real	cdivi

Arrays for internal storage of eigenvalues.
std::vector< Real >	d_

std::vector< Real >	e_

Detailed Description

template<class Real>
class bpp::EigenValue< Real >

Computes eigenvalues and eigenvectors of a real (non-complex) matrix.

[This class and its documentation is adpated from the C++ port of the JAMA library.]

If A is symmetric, then A = V*D*V' where the eigenvalue matrix D is diagonal and the eigenvector matrix V is orthogonal. That is, the diagonal values of D are the eigenvalues, and V*V' = I, where I is the identity matrix. The columns of V represent the eigenvectors in the sense that A*V = V*D.

If A is not symmetric, then the eigenvalue matrix D is block diagonal with the real eigenvalues in 1-by-1 blocks and any complex eigenvalues, a + i*b, in 2-by-2 blocks, [a, b; -b, a]. That is, if the complex eigenvalues look like

        u + iv     .        .          .      .    .
          .      u - iv     .          .      .    .
          .        .      a + ib       .      .    .
          .        .        .        a - ib   .    .
          .        .        .          .      x    .
          .        .        .          .      .    y

then D looks like

          u        v        .          .      .    .
         -v        u        .          .      .    . 
          .        .        a          b      .    .
          .        .       -b          a      .    .
          .        .        .          .      x    .
          .        .        .          .      .    y

This keeps V a real matrix in both symmetric and non-symmetric cases, and A*V = V*D.

The matrix V may be badly conditioned, or even singular, so the validity of the equation A = V*D*inverse(V) depends upon the condition number of V.

(Adapted from JAMA, a Java Matrix Library, developed by jointly by the Mathworks and NIST; see http://math.nist.gov/javanumerics/jama).

Definition at line 105 of file EigenValue.h.

Constructor & Destructor Documentation

◆ EigenValue()

template<class Real>

bpp::EigenValue< Real >::EigenValue ( const Matrix< Real > & A )

inline

Check for symmetry, then construct the eigenvalue decomposition.

Parameters

A	Square real (non-complex) matrix

Definition at line 1110 of file EigenValue.h.

References bpp::EigenValue< Real >::H_, bpp::EigenValue< Real >::hqr2(), bpp::EigenValue< Real >::issymmetric_, bpp::EigenValue< Real >::n_, bpp::EigenValue< Real >::ort_, bpp::EigenValue< Real >::orthes(), bpp::RowMatrix< Scalar >::resize(), bpp::TextTools::toString(), bpp::EigenValue< Real >::tql2(), bpp::EigenValue< Real >::tred2(), and bpp::EigenValue< Real >::V_.

Member Function Documentation

◆ cdiv()

template<class Real>

void bpp::EigenValue< Real >::cdiv	(	Real	xr,
		Real	xi,
		Real	yr,
		Real	yi
	)

inlineprivate

Definition at line 550 of file EigenValue.h.

References bpp::EigenValue< Real >::cdivi, and bpp::EigenValue< Real >::cdivr.

Referenced by bpp::EigenValue< Real >::hqr2().

◆ getD()

template<class Real>

const RowMatrix<Real>& bpp::EigenValue< Real >::getD ( ) const

inline

Computes the block diagonal eigenvalue matrix.

If the original matrix A is not symmetric, then the eigenvalue matrix D is block diagonal with the real eigenvalues in 1-by-1 blocks and any complex eigenvalues, a + i*b, in 2-by-2 blocks, [a, b; -b, a]. That is, if the complex eigenvalues look like

      u + iv     .        .          .      .    .
        .      u - iv     .          .      .    .
        .        .      a + ib       .      .    .
        .        .        .        a - ib   .    .
        .        .        .          .      x    .
        .        .        .          .      .    y

then D looks like

        u        v        .          .      .    .
       -v        u        .          .      .    . 
        .        .        a          b      .    .
        .        .       -b          a      .    .
        .        .        .          .      x    .
        .        .        .          .      .    y

This keeps V a real matrix in both symmetric and non-symmetric cases, and A*V = V*D.

Returns: D: upon return, the matrix is filled with the block diagonal eigenvalue matrix.

Definition at line 1223 of file EigenValue.h.

References bpp::EigenValue< Real >::d_, bpp::EigenValue< Real >::D_, bpp::EigenValue< Real >::e_, and bpp::EigenValue< Real >::n_.

◆ getImagEigenValues()

template<class Real>

const std::vector<Real>& bpp::EigenValue< Real >::getImagEigenValues ( ) const

inline

Return the imaginary parts of the eigenvalues in parameter e.

Returns: e: new matrix with imaginary parts of the eigenvalues.

Definition at line 1188 of file EigenValue.h.

References bpp::EigenValue< Real >::e_.

◆ getRealEigenValues()

template<class Real>

const std::vector<Real>& bpp::EigenValue< Real >::getRealEigenValues ( ) const

inline

Return the real parts of the eigenvalues.

Returns: real(diag(D))

Definition at line 1181 of file EigenValue.h.

References bpp::EigenValue< Real >::d_.

Referenced by bpp::DualityDiagram::compute_(), bpp::MatrixTools::exp(), and bpp::MatrixTools::pow().

◆ getV()

template<class Real>

const RowMatrix<Real>& bpp::EigenValue< Real >::getV ( ) const

inline

Return the eigenvector matrix.

Returns: V

Definition at line 1174 of file EigenValue.h.

References bpp::EigenValue< Real >::V_.

Referenced by bpp::DualityDiagram::compute_(), bpp::MatrixTools::exp(), and bpp::MatrixTools::pow().

◆ hqr2()

template<class Real>

void bpp::EigenValue< Real >::hqr2 ( )

inlineprivate

Definition at line 572 of file EigenValue.h.

References bpp::EigenValue< Real >::cdiv(), bpp::EigenValue< Real >::cdivi, bpp::EigenValue< Real >::cdivr, bpp::EigenValue< Real >::d_, bpp::EigenValue< Real >::e_, bpp::EigenValue< Real >::H_, bpp::EigenValue< Real >::n_, TOST, and bpp::EigenValue< Real >::V_.

Referenced by bpp::EigenValue< Real >::EigenValue().

◆ isSymmetric()

template<class Real>

bool bpp::EigenValue< Real >::isSymmetric ( ) const

inline

Definition at line 1102 of file EigenValue.h.

References bpp::EigenValue< Real >::issymmetric_.

Referenced by bpp::DualityDiagram::compute_().

◆ orthes()

template<class Real>

void bpp::EigenValue< Real >::orthes ( )

inlineprivate

Nonsymmetric reduction to Hessenberg form.

This is derived from the Algol procedures orthes and ortran, by Martin and Wilkinson, Handbook for Auto. Comp., Vol.ii-Linear Algebra, and the corresponding Fortran subroutines in EISPACK.

Definition at line 442 of file EigenValue.h.

References bpp::EigenValue< Real >::H_, bpp::EigenValue< Real >::n_, bpp::EigenValue< Real >::ort_, and bpp::EigenValue< Real >::V_.

Referenced by bpp::EigenValue< Real >::EigenValue().

◆ tql2()

template<class Real>

void bpp::EigenValue< Real >::tql2 ( )

inlineprivate

Symmetric tridiagonal QL algorithm.

This is derived from the Algol procedures tql2, by Bowdler, Martin, Reinsch, and Wilkinson, Handbook for Auto. Comp., Vol.ii-Linear Algebra, and the corresponding Fortran subroutine in EISPACK.

Definition at line 303 of file EigenValue.h.

References bpp::EigenValue< Real >::d_, bpp::EigenValue< Real >::e_, bpp::EigenValue< Real >::n_, and bpp::EigenValue< Real >::V_.

Referenced by bpp::EigenValue< Real >::EigenValue().

◆ tred2()

template<class Real>

void bpp::EigenValue< Real >::tred2 ( )

inlineprivate

Symmetric Householder reduction to tridiagonal form.

This is derived from the Algol procedures tred2 by Bowdler, Martin, Reinsch, and Wilkinson, Handbook for Auto. Comp., Vol.ii-Linear Algebra, and the corresponding Fortran subroutine in EISPACK.

Definition at line 163 of file EigenValue.h.

References bpp::EigenValue< Real >::d_, bpp::EigenValue< Real >::e_, bpp::EigenValue< Real >::n_, and bpp::EigenValue< Real >::V_.

Referenced by bpp::EigenValue< Real >::EigenValue().